DERIVADAS EXPOTENCIALES Y LOGARITMICAS

 

Derivada de la función exponencial

Al igual que cuando encontramos las derivadas de otras funciones, podemos encontrar las derivadas de funciones exponenciales y logarítmicas utilizando fórmulas. A medida que desarrollamos estas fórmulas, necesitamos hacer ciertas suposiciones básicas. Las pruebas que sostienen estos supuestos están más allá del alcance de este curso.

En primer lugar, comenzamos con el supuesto de que la función B(x) = bˣ, b > 0, se define para cada número real y es continua. En cursos anteriores, se definieron los valores de las funciones exponenciales para todos los números racionales, comenzando con la definición de bⁿ, donde n es un número entero positivo, como el producto de b multiplicado por sí mismo n veces. Más tarde, definimos b⁰ = 1, b⁻ⁿ = 1/bⁿ, para un entero positivo n, y bˢ⁄ᵗ = (ᵗ√b)ˢ para enteros positivos s y t. Estas definiciones dejan abierta la cuestión del valor de bʳ donde r es un número real arbitrario. Al suponer la continuidad de B(x) = bˣ, b > 0, podemos interpretar bʳ como limx → r bˣ donde los valores de x tiende a números racionales. Por ejemplo, podemos ver como el número que satisface

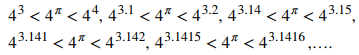
Como vemos en la siguiente tabla, 4^ π ≈ 77.88.

Tabla 3.9_1 Aproximación de un valor de 4^π

También suponemos que para B(x) = bˣ, b > 0, existe el valor B′(0) de la derivada. En esta sección, mostramos que al hacer esta suposición adicional, es posible demostrar que la función B(x) es diferenciable en todas partes.

Hacemos una suposición final: que hay un valor único de b > 0 para el cual B′(0) = 1. Definimos e como este valor único, como lo hicimos en Introducción a funciones y sus gráficas. La figura 3.9_1 proporciona gráficas de las funciones y = 2ˣ, y = 3ˣ, y = 2.7ˣ, y y = 2.8ˣ. Una estimación visual de las pendientes de las rectas tangentes a estas funciones en 0 proporciona evidencia de que el valor de e se encuentra entre 2.7 y 2.8. La función E(x) = eˣ se llama función exponencial natural. Su inverso, L(x) = logex = lnx se llama función logaritmo natural.

Para una mejor estimación de e, podemos construir una tabla de estimaciones de B′(0) para funciones de la forma B(x) = bˣ. Antes de hacer esto, recuerda que

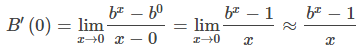
para valores de x muy cercanos a cero. Para nuestras estimaciones, elegimos x = 0.00001 y x = −0.00001 para obtener la estimación

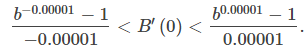
Ver la siguiente tabla:

REGLAS TRIGONOMETRICAS

 REGLAS TRIGONOMETRICAS

Las derivadas de funciones trigonométricas son otras funciones trigonométricas. Por ejemplo, la derivada de la función seno es igual a la función coseno y la derivada de la función coseno es igual a seno negativo.

A continuación, conoceremos todas las fórmulas de las derivadas de las funciones trigonométricas. Además, veremos algunos ejercicios en donde aplicaremos estas fórmulas.

Fórmulas de las derivadas de funciones trigonométricas

Derivada de la función seno

La derivada de la función seno estándar es:

${\sin }^{\mathrm{\prime }}(𝑥)=\cos (𝑥)$

Para derivar a funciones seno de la forma $\sin (𝑛𝑥)$, usamos la regla de la cadena con $𝑦=\sin (𝑢)$ y $𝑢=𝑛𝑥$.

De igual forma, para derivar funciones de la forma ${\sin }^{𝑛}(𝑥)=(\sin (𝑥){)}^{𝑛}$, usamos la regla de la cadena con $𝑦={𝑢}^{𝑛}$ y $𝑢=\sin (𝑥)$.

Derivada de la función coseno

La derivada de la función coseno estándar es:

${\cos }^{\mathrm{\prime }}(𝑥)=-\sin (𝑥)$

Si tenemos funciones de la forma $\cos (𝑛𝑥)$, podemos usar la regla de la cadena con $𝑦=\cos (𝑢)$ y $𝑢=𝑛𝑥$.

En el caso de funciones de la forma ${\cos }^{𝑛}(𝑥)=(\cos (𝑥){)}^{𝑛}$, usamos la regla de la cadena con $𝑦={𝑢}^{𝑛}$ y $𝑢=\cos (𝑥)$.

Derivada de la función tangente

La derivada de la función tangente estándar es:

${\tan }^{\mathrm{\prime }}(𝑥)={\sec }^2(𝑥)$

Para funciones de la forma $\tan (𝑛𝑥)$, usamos la regla de la cadena con $𝑦=\tan (𝑢)$ y $𝑢=𝑛𝑥$.

Para funciones de la forma ${\tan }^{𝑛}(𝑥)=(\tan (𝑥){)}^{𝑛}$, usamos la regla de la cadena con $𝑦={𝑢}^{𝑛}$ y $𝑢=\tan (𝑥)$.

Derivada de la función cosecante

La derivada de la función cosecante estándar es:

${\mathrm{cosec}}^{\mathrm{\prime }}(𝑥)=-\mathrm{cosec}(𝑥)\cot (𝑥)$

Las funciones cosecante de la forma $\mathrm{cosec}(𝑛𝑥)$, pueden ser derivadas con la regla de la cadena al usar $𝑦=\mathrm{cosec}(𝑢)$ y $𝑢=𝑛𝑥$.

De igual forma, las funciones de la forma ${\mathrm{cosec}}^{𝑛}(𝑥)=(\mathrm{cosec}(𝑥){)}^{𝑛}$, son derivadas con la regla de la cadena con $𝑦={𝑢}^{𝑛}$ y $𝑢=\mathrm{cosec}(𝑥)$.

Derivada de la función secante

La derivada de la función secante estándar es:

${\sec }^{\mathrm{\prime }}(𝑥)=\sec (𝑥)\tan (𝑥)$

Las funciones secante de la forma $\sec (𝑛𝑥)$ son derivadas usando la regla de la cadena con $𝑦=\sec (𝑢)$ y $𝑢=𝑛𝑥$.

De igual forma, las funciones de la forma ${\sec }^{𝑛}(𝑥)=(\sec (𝑥){)}^{𝑛}$ son derivadas usando la regla de la cadena con $𝑦={𝑢}^{𝑛}$ y $𝑢=\sec (𝑥)$.

Derivada de la función cotangente

La derivada de la función cotangente estándar es:

${\cot }^{\mathrm{\prime }}(𝑥)=-{\mathrm{cosec}}^2(𝑥)$

Para derivar a funciones cotangente de la forma $\cot (𝑛𝑥)$, aplicamos la regla de la cadena con $𝑦=\cot (𝑢)$ y $𝑢=𝑛𝑥$.

Las funciones de la forma ${\cot }^{𝑛}(𝑥)=(\sin (𝑥){)}^{𝑛}$, también son derivadas usando la regla de la cadena con $𝑦={𝑢}^{𝑛}$ y $𝑢=\cot (𝑥)$

Ejercicios resueltos de derivadas de funciones trigonométricas

EJERCICIO 1

Encuentra la derivada de $𝑦=\sin (5𝑥)$.

Solución

Podemos usar la regla de la cadena con $𝑢=5𝑥$. Entonces, tenemos:

$𝑦=\sin (𝑢)$ y $𝑢=5𝑥$

sus derivadas son:

${\displaystyle \frac{𝑑𝑦}{𝑑𝑢}}=\cos (𝑢)$ y ${\displaystyle \frac{𝑑𝑢}{𝑑𝑥}}=5$

Ahora, aplicamos la regla de la cadena:

$$\frac{𝑑𝑦}{𝑑𝑥}=\frac{𝑑𝑦}{𝑑𝑢}\frac{𝑑𝑢}{𝑑𝑥}=\cos (𝑢)\times 5$$

$$\frac{𝑑𝑦}{𝑑𝑥}=5\cos (5𝑥)$$

Generalmente, escribimos de la siguiente forma para encontrar la respuesta más rápido:

$$\frac{𝑑𝑦}{𝑑𝑥}=\cos (5𝑥)\times (5𝑥{)}^{\mathrm{\prime }}=5\cos (5𝑥)$$

EJERCICIO 2

Encuentra la derivada de $𝑦={\cos }^2(𝑥)$.

Solución

Podemos empezar escribiendo como $(\cos (𝑥){)}^2$. Luego, tenemos:

$𝑦={𝑢}^2$ y $𝑢=\cos (𝑥)$

Las derivadas son:

${\displaystyle \frac{𝑑𝑦}{𝑑𝑢}}=2𝑢$ y ${\displaystyle \frac{𝑑𝑢}{𝑑𝑥}}=-\sin (𝑥)$

Usando la regla de la cadena, tenemos:

$$\frac{𝑑𝑦}{𝑑𝑥}=\frac{𝑑𝑦}{𝑑𝑢}\frac{𝑑𝑢}{𝑑𝑥}=2𝑢(-\sin (𝑥))$$

$$\frac{𝑑𝑦}{𝑑𝑥}=-2\cos (𝑥)\sin (𝑥)$$

Generalmente, escribimos de la siguiente forma para encontrar la respuesta más rápido:

$$\frac{𝑑𝑦}{𝑑𝑥}=2\cos (𝑥)\times (\cos (𝑥){)}^{\mathrm{\prime }}=-2\cos (𝑥)\sin (𝑥)$$